A série 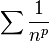 converge se
converge se  e diverge se
e diverge se  .
.
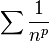 converge se
converge se  e diverge se
e diverge se  .
.
série infinitesimais de Graceli .
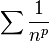 [f [ log cc/cc [lsg]]], +
[f [ log cc/cc [lsg]]], + 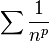 [f [ log cc/cc [lsg]]],
[f [ log cc/cc [lsg]]], 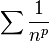 [[f [ log cx/cx [lsg]]]./
[[f [ log cx/cx [lsg]]]./ 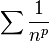 [[f [ log cx/cx [lsg]]]
[[f [ log cx/cx [lsg]]]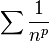 [[f [ log cx/cx [lsg]]] , .[[f [ log cc/cc [lsg]]].
[[f [ log cx/cx [lsg]]] , .[[f [ log cc/cc [lsg]]].
p = progressão.
côncavo e convexo.
p/pP [n]
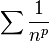 [[f [ log π/π [lsg]]],
[[f [ log π/π [lsg]]], 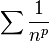 [[f [ log seno x/seno x [lsg]]].
[[f [ log seno x/seno x [lsg]]]. 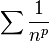 [[f [ log seno x/seno x [lsg]]].
[[f [ log seno x/seno x [lsg]]]. 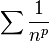 [[f [ pP[n] seno x/seno x [lsg]]].
[[f [ pP[n] seno x/seno x [lsg]]].
Nenhum comentário:
Postar um comentário